我が国における超過死亡の推定（2020年4月までのデータ分析）
掲載日：2020年7月31日
要約
2012年～2020年の人口動態統計データを用いて、日本における新型コロナウイルス感染症流行期（2020年1月～4月末）の超過死亡を週別、都道府県別に推定した。欧米諸国と我が国における比較可能性を考慮し、米国疾病予防管理センター（Centers for Disease Control and Prevention：CDC）の用いるFarringtonアルゴリズム、および欧州死亡率モニター（EuroMOMO）の用いるFluMOMOモデルを用いた。結果、Farringtonアルゴリズムで超過死亡が検出されたのは、千葉県（47人：4月20日–26日、疫学週第17週）のみであった。またEuroMOMOアルゴリズムでは、栃木県（14人：2019年12月30日–2020年1月5日、疫学週第1週）、埼玉県（5人：4月13日–19日、疫学週第16週）、千葉県（61人：4月20日–26日、疫学週第17週）、東京都（55人：4月13日–19日、疫学週第16週）、徳島県（3人：4月13日–19日、疫学週第16週）で超過死亡が検出された。今後、死因を考慮した解析の有効性、環境因子を考慮した解析の検討を行う。
※結果をご覧いただく際の注意事項
本分析で観察された超過死亡は以下の内訳等の死亡の総和と解釈できる： １）新型コロナウイルス感染症を直接死因と診断され、（実際に）新型コロナウイルス感染症を原因とする死亡、２）新型コロナウイルス感染症を直接死因と診断されなかった（他の病因を直接死因と診断された）が、（実際には）新型コロナウイルス感染症を原因とする死亡、３）新型コロナウイルス感染症を直接死因と診断されず、（新型コロナ流行による間接的な影響で）他の病因を原因とする死亡（例えば、病院不受診や生活習慣の変化に伴う持病の悪化による死亡）。一方で、同時期に新型コロナウイルス感染症以外を直接死因とする死亡（例えば、交通事故死、自殺、インフルエンザ等他の感染症による死亡）が過去の同時期より減少した場合、新型コロナウイルス感染症を直接死因とする超過死亡を相殺することがあり得る。
FarringtonアルゴリズムとEuroMOMOアルゴリズムはどちらも既に実証、確立、実用されている手法であり、妥当性に関する優劣はつけ難い。Farringtonアルゴリズムのほうが保守的な結果、つまり超過死亡が出にくくなる統計的な計算結果が返されることが認められた。一方でEuroMOMOアルゴリズムは比較的に超過死亡は出やすくなる。これらのことを勘案し、両アルゴリズムの結果の間に真の超過死亡数があるだろう、と結論付けるのが良いと考える。
1 背景
温帯地域においてインフルエンザが大きく流行した冬は、流行の小さな冬に比べ死亡者数が増える現象は古くより観察されており、インフルエンザを直接死因とする死亡の増加のみならず、呼吸器疾患や循環器疾患など様々な疾患による死亡が増加することが知られている。このようなインフルエンザ以外の死因も含め、ある人口集団における死者数に対するインフルエンザ流行のインパクトを把握する目的で超過死亡の概念が用いられてきた。1973年にWHO(1)がインフルエンザ発生動向の監視や包括的健康影響評価を目的として超過死亡の概念を提唱して以降、世界的に広くその推定が行われてきた。我が国においても、インフルエンザ関連死亡者迅速把握事業等において1998年より超過死亡の推定が行われてきた(2)。新型コロナウイルス感染症の流行に伴い、米国CDC(3)やヨーロッパ24か国が参加するEuroMOMOネットワーク(4)などでは超過死亡推定法および推定結果を公表しており、我が国においても同様の対応が求められる。なお、本文書は新たな知見等を踏まえ、適宜更新することとする。
2 目的
日本における新型コロナウイルス感染症による超過死亡を推定する。
3 超過死亡推定法
本稿における超過死亡の定義は、特定の集団において、新型コロナウイルス感染症流行期（2020年1月以降）に、例年同時期の死亡数をもとに推定される死亡数（予測死亡数）の95%片側予測区間（上限）と実際の死亡数（観測死亡数）との差とする。ここで、「死亡数」が指すのは全死亡であり、新型コロナウイルス感染症のみならず特定の疾患に起因する死亡に限定しない。
超過死亡の推定方法は、主なものでは、Serflingらの方法(5, 6)、Choiらの方法(7, 8)、河合・福富らの方法(9, 10)、Simonsenらの方法(11)、高橋らの方法(12)、感染研の方法(13)などが提案されている(14)。これらの方法はいずれもインフルエンザの流行による超過死亡推定を目的としており、インフルエンザ非流行時の死亡数をもとに予測死亡数を推定し、観測死亡数から減じることで超過死亡を求めている。一方で、米国CDC、欧州EuroMOMOでは、それぞれFarringtonアルゴリズム、FluMOMOモデルを用いて新型コロナウイルス感染症による超過死亡の推定を行っており、既に公表済みのこれら欧米諸国の超過死亡と我が国の超過死亡を比較することを考慮し、本報告ではCDCおよびEuroMOMOの解析法を用いて超過死亡を推定する。表１に各推定法の超過死亡表現法と採用モデルを記す。
表1：超過死亡の推定方法（文献１４の表1を改編）| 方法 | 超過死亡の表現法 | 採用しているモデル |
| Serflingらの方法 | インフルエンザの流行がない場合の死亡数の期待値と実際の死亡数との差 | 月数と三角関数sin, cosを用いた回帰曲線モデル |
| Choiらの方法 | 同上 | 季節ARIMAモデル |
| 河合・福富らの方法 | 同上 | 年間死亡率と季節指数を用いたモデル |
| 感染研の方法 | インフルエンザの流行がない場合の死亡数の95%予測区間※１上限値と実際の死亡数との差 | 確率的フロンティア推定モデル |
| 高橋らの方法 | インフルエンザの流行がない場合の死亡数の95%範囲※１上限値と実際の死亡数との差 | 年間死亡率と季節指数を用いたモデル |
| Simonsenらの方法 | インフルエンザの流行がない場合の死亡数の95%予測区間※１限界値（下限値、上限値）と実際の死亡数との差 | 月数と三角関数sin, cosを用いた回帰曲線モデル |
| Farringtonらの方法 （米CDC) | 例年同時期の死亡数をもとに推定される死亡数の95%片側予測区間（上限）と実際の死亡数（観測死亡数）との差 | 過去数年間の同じ週の前後数週間の区間データを主に用いてモデルの係数を推定（Quasi-Poisson regression）。それ以外の区間は季節性の調整のためにダミー変数として入れることも可能。 |
| EuroMOMOの方法 | 過去全期間の死亡数をもとに推定される死亡数の95%両側予測区間（上限）と実際の死亡数（観測死亡数）との差 | 週数とフーリエ項を用いた回帰モデル（Quasi-Poisson regression） |
| ※１ インフルエンザの流行がない場合の死亡数（実現値）が0.95の確率でとると考えられる値の範囲 | ||
3.1 利用データ
今回の超過死亡推定では、統計法第32条の調査票情報の提供による、厚生労働省人口動態調査における死亡票データを利用する。当該調査では、「戸籍法」および「死産の届出に関する規定」により届け出られた出生、死亡、婚姻、離婚及び死産の全数を対象としている。
人口動態調査死亡票における確定数は調査年の翌年9月、概数のうち毎月のデータは調査月の約5か月後、毎年のデータ（年間合計）は調査年の翌年6月上旬、速報は調査月の約2か月後に公表されている。なお、都道府県別死亡数は、速報については死亡届が届け出られた都道府県に、概数や確定数については住所地の都道府県に計上している。ただし、死亡地となる都道府県の情報は人口動態調査では把握できていない。
本分析では、東日本大震災(2011年)による一時的な死亡数増加によるバイアスの可能性を除くため、2012年以降のデータを用いることとする（予測死亡数推定にあたり、2012年以降の外れ値の除外は行わない）。2012年から2018年は確定数、2019年は概数、2020年1月分以降は速報を利用する。なお、初回の報告では2020年4月分までのデータを利用する。概数および速報は暫定値であり今後修正される可能性がある。
本分析は、2012年から2018年の確定数、および2019年の概数データについては、集計客体（符号表項目名’客体設定’）が「日本における日本人」および「日本における外国人」のデータを利用する。また、都道府県別に行う都合、都道府県別分類（符号表項目名’都道府県’）が不詳のデータについては分析から除外する。また、2020年1月分以降の速報データについては、集計客体の項目がまだ付与されていないため、死亡場所（符号表項目名’国内外（死亡したところ）’）が海外、あるいは都道府県別分類（符号表項目名’都道府県’）が外国または不詳のデータを分析から除外することで、「日本における日本人」および「日本における外国人」のデータを同定する。都道府県別分類は住所地に基づくため、観光目的など短期滞在者の外国人は分析に含まれない。日別データから週別データへの変換は、国立感染症研究所の感染症発生動向調査週報の疫学週を用いる(15)。
（参考：厚生労働省ホームページ，人口動態調査・調査の概要 https://www.mhlw.go.jp/toukei/list/81-1b.html#05）
3.2 Farringtonアルゴリズム（CDC）
Farringtonアルゴリズムは、超過死亡を推定するために用いられる一般的な手法の一種であり、CDCでは、新型コロナウイルスに関連する超過死亡の推定に用いられている。本手法は、週毎の死亡の(1)傾向および不確実性の推定と、(2)予測および超過判定の二段階で構成されている。詳しい手法はFarrington et al. (1996)(16)およびNofaily et al. (2013)(17)を参照。
まず、(1)傾向および不確実性の推定（dispersionパラメータ及び予測区間）についての概略を説明する。推定にはCDCの方法論に倣い、週あたりの死亡数を推定するためのquasi-Poisson regression（カウントデータの過分散（Over-dispersion）に対応するための一般化線形モデルの一種）を用いる。その際、推定に主に用いるデータを時間ごとに限定する。具体的には、ある時点（週）tから「数年前」の「予測したい週の前後数週間」（ウィンドウ期間と呼ぶ）のデータを主に用いてモデルの係数の推定を行う。後述の通り、ウィンドウ期間外のデータも推定する際のデータに含めることも可能である。次に推定された回帰係数（モデルの定式化は以下）を用いてモデルの不確実性を表すパラメータ（quasi-Poissonのdiseprsionパラメータ）を計算し、最終的に予測区間を構成する。最後に本研究では、季節性を考慮するために、1年のうちウィンドウ期間に入らなかった時点のデータを等分割してダミー変数として回帰モデルの中に含める。モデルの定式化は以下。
ただし、E( ) は期待値演算、Yt はある時点（週）tにおける死亡者数、α, βは回帰パラメータ（スカラー）、 
は季節性を表す項でウィンドウ期間外の時点を等分割（本研究では9分割）しダミー化したベクトル、 
はダミー変数に対応する回帰パラメータ（ベクトル）である。本研究においては、5年前までの前後3週間をデータとして用いて推定を行う（Rコード内の補足資料1ではそれぞれb=5、w=3を設定）。感度分析としてこのウィンドウ期間を変化させその結果の頑健性を確認する（b=3,4およびw=2,4を検討）。
次に(2)予測および超過判定について説明する。(1)で推定した回帰モデルを用いて、予測死亡数を点推定し、同時に推定の不確かさの指標である95%片側予測区間（上限）を算出する（統計学的に予測死亡数の取り得る範囲の上限値）。
観測死亡数と95%片側予測区間（上限）の値を比較し、観測死亡数がそれらを超過した場合、超過死亡としてフラグを立てる（超過死亡数＝観測死亡数と95%片側予測区間（上限）の差）。また、その超過死亡数の不確かさの尺度評価として、超過死亡上限値として観測死亡数と点推定した予測死亡数の差を求め、補足資料で提示する。以上がFarringtonアルゴリズムの概略である。なお、本アルゴリズムのRコードは補足資料1を参照。
3.3 EuroMOMOアルゴリズム
EuroMOMOネットワークでは超過死亡推定に通常FluMOMOモデルを用いている。同モデルの詳細はEuroMOMOウェブサイト(18)、出版物(19, 20, 21)を参照。
本モデルはquasi-Poisson regressionを用いた時系列解析である。2012年1月～2020年1月の週別死亡者数時系列データを用いて、2020年1月～4月の予測死亡数を推定した。三角関数sin, cosを用いて過去に毎年繰り返される（死亡数の）季節性をモデル化し、当該年度の同期間も同じ季節性が再現されると仮定し、予測死亡数を推定するものである。季節性のモデル化にあたっては、1年および6か月間を1周期とする、周期の異なるsin, cos波をそれぞれモデルに投入した。高齢化にともなう死亡数の経年増加や年々変化する環境要因等の影響を考慮する目的で、週の線形項を用いて長期トレンドをモデル化した。
モデル式を以下に示す。
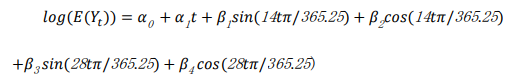
E( ) は期待値演算、α, β は回帰パラメータ（スカラー）、Yt はある時点（週）t における死亡者数を表す。感度分析としてこの線形項t を自然3次スプラインに拡張し、その自由度を2もしくは3と変化させ、結果の頑健性を確認する。
残差を2/3乗することで正規近似を行い、95%片側予測区間（上限）を求めた上で、観測死亡数と95%片側予測区間（上限）の値を比較し、観測死亡数がそれらを超過した場合、超過死亡としてフラグを立てる（超過死亡数＝観測死亡数と95%片側予測区間（上限）の差）。また、その超過死亡数の不確かさの尺度評価として、超過死亡上限値として観測死亡数と点推定した予測死亡数の差を求め、補足資料で提示する。なお、本アルゴリズムのRコードは補足資料2を参照。
3.4 速報の補正
死亡票の速報において報告遅れの補正方法について検討する。ここで報告遅れとはある月の死亡データが1ヶ月以上遅れて報告されることを指す。
本推定（7月末時点）では、速報データとして1–4月までのデータを利用しており、ここから各月の報告遅れを推定することを考える。米国CDCではzero-inflated binomial hierarchical Bayesian models などを用いて報告遅れをモデル化しているが、本推定では4ヶ月の月次データしかないことを考えると、このようなパラメータ数の多いモデルは推定困難である。したがって、本研究ではシンプルな報告遅れの補正モデルを考える。また上記のような使用可能なデータの制約から以下のような仮定をおく。
仮定1：報告遅れは最大3ヶ月まで
仮定2：報告遅れに季節性や月別の特性などはない
仮定3：月内の報告遅れは、その月内では一様に分布する
ある県i (都道府県番号)の時点t の時点d における報告死亡数を 
とする。例えば、月次データを考えると、東京都(都道府県番号i=13)の1月の死亡者数が3月に遅れて報告された場合は 
と記述する。ある県iにおいて報告遅れは以下の報告行列 
の上三角成分として表現可能である。 の行は死亡月を、列は報告月を表す。以下は、1–4月の場合の例を示す。
我々は7月現在、この の情報を保持しており、ここから1–4月の報告遅れの数を推定する問題を考える。仮定1より1月は全ての報告遅れはあるものの、それらは全て報告済みであると考える。したがって仮定1より、推定すべきは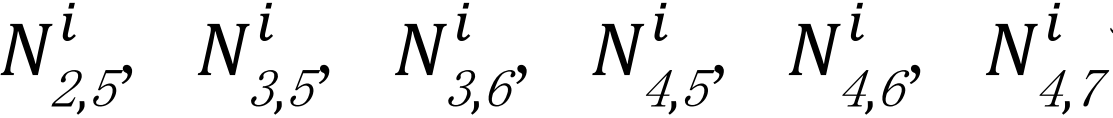 
である。仮定2より各月の報告遅れは同一の分布に従うと考えられることを念頭に置き、以下のような推定量を提案する。
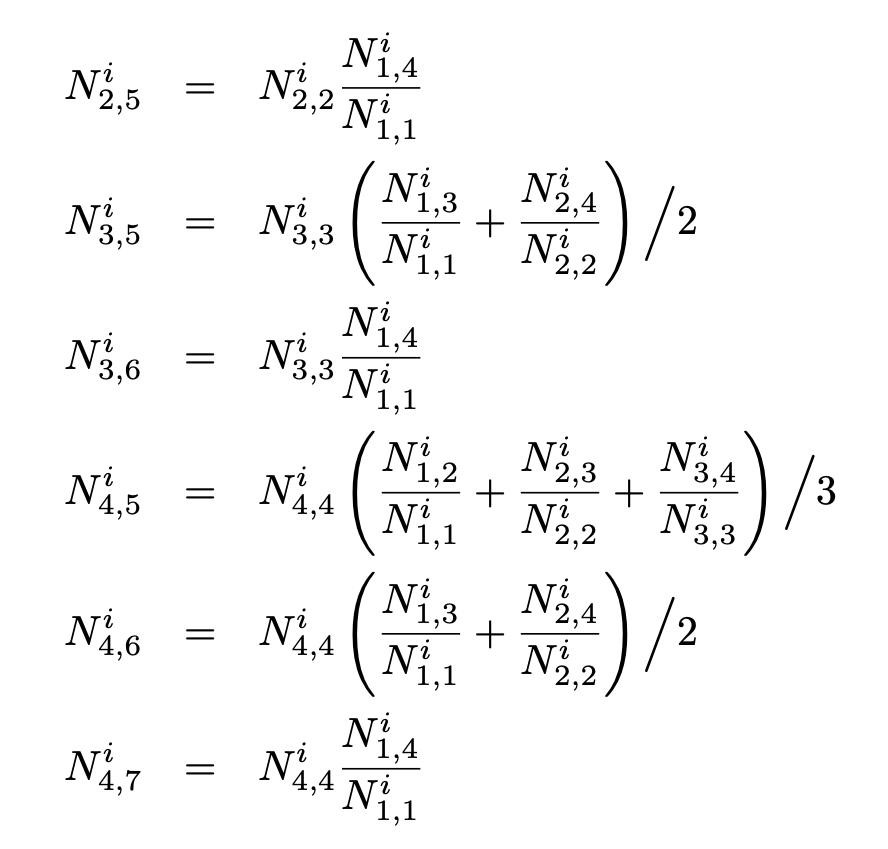
現在は1–4月で考えているが、今後新しいデータが来た場合でも、ある連続する4ヶ月(仮定1)を切り出し、その最初の月を報告行列の1月成分と再定義することで一般化可能である。
次に推定された報告遅れの死亡者数を用いて、県iにおける各月の報告遅れ割合を以下のように推定する。
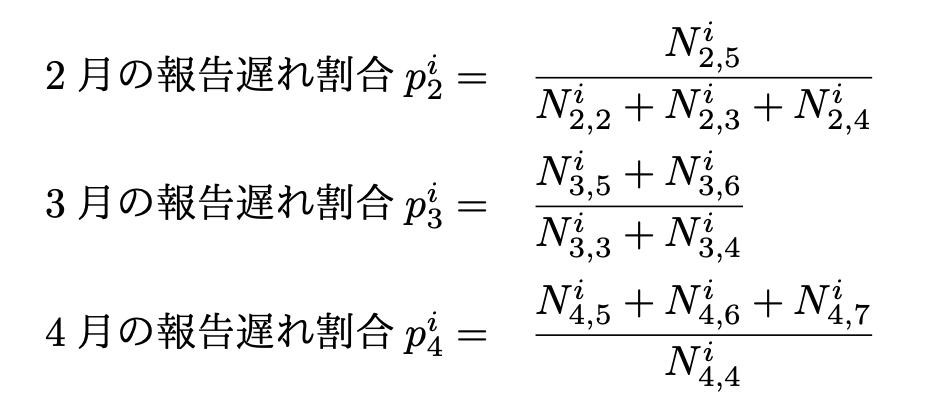
最後に死亡表の個票(日毎データ)を週別に集計する際に各月毎に推定された報告遅れ割合を加重しながら集計することで報告遅れ補正済みデータとして扱う。ある月内では月頭も月末も同じ重みをかけることは仮定3より正当化される。
特に断りのない限り、本超過死亡推定の結果はこの補正済みデータを用いた推定結果である。また、本分析に使用された都道府県別の週別の死亡者数、および速報の補正済みデータは、補足資料3を参照。
4 結果
4.1 Farrington アルゴリズム
2020年1月以降（感染研疫学週における第1週＝2019年12月30日–2020年1月5日から）、超過死亡が検出されたのは、千葉県（47人：4月20日–26日、疫学週第17週）のみであった。表2は都道府県別の超過死亡数のリストである。週別の超過死亡は別添図1（補正あり）、図2（補正なし）を参照。
図1：Farrington アルゴリズムに基づく週別の超過死亡、速報の補正あり（2017年から。十字は超過死亡フラグ＝観測死亡数＞95%片側予測区間（上限）の値）
図2：Farrington アルゴリズムに基づく週別の超過死亡、速報の補正なし（2017年から。十字は超過死亡フラグ＝観測死亡数＞95%片側予測区間（上限）の値）
4.2 EuroMOMOアルゴリズム
2020年1月以降、速報補正後に超過死亡が検出されたのは、栃木県（14人：2019年12月30日–2020年1月5日：疫学週第1週）、埼玉県（5人：4月13日–19日、疫学週第16週）、千葉県（61人：4月20日–26日、疫学週第17週）、東京都（55人：4月13日–19日、疫学週第16週）、徳島県（3人：4月13日–19日、疫学週第16週）であった。表2は都道府県別の超過死亡数のリストである。週別の超過死亡は別添図3（補正あり）、図4（補正なし）を参照。
図3：EuroMOMOアルゴリズムに基づく週別の超過死亡、速報の補正あり（2017年から。十字は超過死亡フラグ＝観測死亡数＞95%片側予測区間（上限）の値）
図4：EuroMOMOアルゴリズムに基づく週別の超過死亡、速報の補正なし（2017年から。十字は超過死亡フラグ＝観測死亡数＞95%片側予測区間（上限）の値）
なお表2の超過死亡推定値は、両アルゴリズムで推定された2020年1月から4月までの週別の超過死亡の積算であり（初週は2019年12月30–31日含み、最終週は4月26日までである）、CDCの方法論に倣い、観測値が95%片側予測区間（上限）を超えていない場合はゼロとしてカウントしている。同様に、全国の超過死亡推定値は、各都道府県の推定値を積算している。
図1–4の週別の超過死亡の実数は、補足資料4を参照。表2の全国の超過死亡と図1–4における全国の超過死亡は一致しない：前者は47都道府県別の超過死亡の積算を全国の超過死亡としているのに対し、後者は47都道府県別の観測死亡数、予測死亡数、95%片側予測区間を毎週ごとに積算した上で、超過死亡のフラグを立てているためである。
表2：2020年1月から4月までのFarringtonアルゴリズムおよびEuroMOMOアルゴリズムに基づく推定超過死亡
| Farrington | EuroMOMO | |||
| 速報補正 | あり | なし | あり | なし |
| 北海道 | 0 | 0 | 0 | 0 |
| 青森 | 0 | 0 | 0 | 0 |
| 岩手 | 0 | 0 | 0 | 0 |
| 宮城 | 0 | 0 | 0 | 0 |
| 秋田 | 0 | 0 | 0 | 0 |
| 山形 | 0 | 0 | 0 | 0 |
| 福島 | 0 | 0 | 0 | 0 |
| 茨城 | 0 | 0 | 0 | 0 |
| 栃木 | 0 | 0 | 14 | 14 |
| 群馬 | 0 | 0 | 0 | 0 |
| 埼玉 | 0 | 0 | 5 | 0 |
| 千葉 | 47 | 28 | 61 | 42 |
| 東京 | 0 | 0 | 55 | 0 |
| 神奈川 | 0 | 0 | 0 | 0 |
| 新潟 | 0 | 0 | 0 | 0 |
| 富山 | 0 | 0 | 0 | 0 |
| 石川 | 0 | 0 | 0 | 0 |
| 福井 | 0 | 0 | 0 | 0 |
| 山梨 | 0 | 0 | 0 | 0 |
| 長野 | 0 | 0 | 0 | 0 |
| 岐阜 | 0 | 0 | 0 | 0 |
| 静岡 | 0 | 0 | 0 | 0 |
| 愛知 | 0 | 0 | 0 | 0 |
| 三重 | 0 | 0 | 0 | 0 |
| 滋賀 | 0 | 0 | 0 | 0 |
| 京都 | 0 | 0 | 0 | 0 |
| 大阪 | 0 | 0 | 0 | 0 |
| 兵庫 | 0 | 0 | 0 | 0 |
| 奈良 | 0 | 0 | 0 | 0 |
| 和歌山 | 0 | 0 | 0 | 0 |
| 鳥取 | 0 | 0 | 0 | 0 |
| 島根 | 0 | 0 | 0 | 0 |
| 岡山 | 0 | 0 | 0 | 0 |
| 広島 | 0 | 0 | 0 | 0 |
| 山口 | 0 | 0 | 0 | 0 |
| 徳島 | 0 | 0 | 3 | 2 |
| 香川 | 0 | 0 | 0 | 0 |
| 愛媛 | 0 | 0 | 0 | 0 |
| 高知 | 0 | 0 | 0 | 0 |
| 福岡 | 0 | 0 | 0 | 0 |
| 佐賀 | 0 | 0 | 0 | 0 |
| 長崎 | 0 | 0 | 0 | 0 |
| 熊本 | 0 | 0 | 0 | 0 |
| 大分 | 0 | 0 | 0 | 0 |
| 宮崎 | 0 | 0 | 0 | 0 |
| 鹿児島 | 0 | 0 | 0 | 0 |
| 沖縄 | 0 | 0 | 0 | 0 |
| 全国 | 47 | 28 | 138 | 58 |
以上をまとめると、複数の都県において、数人から50～60人程度の超過死亡が2020年4月に観察された。多くの道府県においては、超過死亡は検出されなかった。
観測死亡数と予測死亡数の差（超過死亡上限値）は補足資料5を参照、さらにFarringtonアルゴリズムおよびEuroMOMOアルゴリズムの感度分析の結果はそれぞれ補足資料6、7を参照。
5 超過死亡の解釈
観察された超過死亡は以下の内訳等の死亡の総和と解釈できる。
1) 新型コロナウイルス感染症を直接死因と診断され、（実際に）新型コロナウイルス感染症を原因とする死亡
2) 新型コロナウイルス感染症を直接死因と診断され、（実際には）新型コロナウイルス感染症を原因としない死亡（例えば、実際の死因はインフルエンザだが、新型コロナウイルス感染症が死因と診断された死亡。新型コロナウイルス感染症の診断がPCR検査に基づく現状では、ほぼ該当例はないと考えられる。）
3) 新型コロナウイルス感染症を直接死因と診断されず（他の病因を直接死因と診断された）、（実際には）新型コロナウイルス感染症を原因とする死亡
4) 新型コロナウイルス感染症を直接死因と診断されず、（新型コロナ流行による間接的な影響で）他の病因を原因とする死亡（例えば、病院不受診や生活習慣の変化に伴う持病の悪化による死亡）
一方で、同時期に新型コロナウイルス感染症以外を原因とする死亡（例えば、交通事故死、自殺、インフルエンザ等他の感染症による死亡）が過去の同時期より減少した場合、新型コロナウイルス感染症を直接死因とする超過死亡を相殺することがあり得る。
FarringtonアルゴリズムとEuroMOMOアルゴリズムに基づく超過死亡の推定結果の差異については、アルゴリズム（予測死亡数や95%片側予測区間の推定方法）が異なるので結果に多少違いが生じることは想定される。どちらの方法論も既に実証、確立、実用されている手法であり、優劣はつけ難い。Farringtonアルゴリズムのほうが保守的な結果、つまり超過死亡が出にくくなる統計的な計算結果が返されることが認められた。一方でEuroMOMOアルゴリズムは比較的に超過死亡は出やすくなる。これらのことを勘案して両者を併記し、FarringtonアルゴリズムとEuroMOMOアルゴリズムの両者の結果の間に真の超過死亡数があるだろう、と結論付けるのが良いと考える。
6 今後の課題
6.1 死因を考慮した超過死亡推定
今回は全死亡の超過死亡を推定したが、2020年各月の概数値データが得られ次第、必要に応じて以下の死因を考慮した解析の有効性等を検討する。
- 交通事故死、自殺等の外因死を除いた解析
- 特定疾患（肺炎等）の超過死亡
6.2 環境因子等を考慮した超過死亡推定
気温およびインフルエンザの流行は死亡数に影響を及ぼすことが知られており、これら環境因子等を考慮した解析を今後検討する。
- 気温（暑さ・寒さ）の影響を補正後の超過死亡を推定。気温の影響を考慮する際、測定誤差を小さくするため、日別解析を行などの工夫が必要となる。
- 感染症発生動向調査週報 (IDWR)や病原微生物検出情報 (IASR)を用いてインフルエンザ流行の影響を補正後、超過死亡を推定
6.3 既存推定法の日本への適用の妥当性評価、日本のデータに適した算定法の開発
7 引用文献
- Assaad F, Cockburn WC, Sundaresan TK. Use of excess mortality from respiratory diseases in the study of influenza. Bulletin of the World Health Organization. 1973;49(3):219-33.
- 国立感染症研究所. インフルエンザ関連死亡迅速把握システム [https://www.niid.go.jp/niid/index.php/ja/ja/flu-m/flutoppage/2112-idsc/jinsoku/131-flu-jinsoku.html].
- Centers for Disease Control and Prevention. Excess Deaths Associated with COVID-19 2020 [https://www.cdc.gov/nchs/nvss/vsrr/covid19/excess_deaths.htm].
- EuroMOMO network. [www.euromomo.eu].
- Serfling RE, Sherman IL, Houseworth WJ. Excess pneumonia-influenza mortality by age and sex in three major influenza A2 epidemics, United States, 1957-58, 1960 and 1963. Am J Epidemiol. 1967;86(2):433-41.
- Serfling RE. Methods for current statistical analysis of excess pneumonia-influenza deaths. Public Health Rep. 1963;78(6):494-506.
- Choi K, Thacker SB. Mortality during influenza epidemics in the United States, 1967-1978. Am J Public Health. 1982;72(11):1280-3.
- Choi K, Thacker SB. An evaluation of influenza mortality surveillance, 1962-1979. I. Time series forecasts of expected pneumonia and influenza deaths. Am J Epidemiol. 1981;113(3):215-26.
- 河合 道, 福富和夫, 杉浦 昭. インフルエンザと超過死亡（1966～1978）. 臨床とウイルス. 1980;8:53-6.
- 福富和夫, 橋本修二. 季節変動の観察—インフルエンザによる超過死亡. 保健統計・疫学. 東京: 南山堂; 2005. p. 56-7.
- Simonsen L, Clarke MJ, Williamson GD, Stroup DF, Arden NH, Schonberger LB. The impact of influenza epidemics on mortality: introducing a severity index. American Journal of Public Health. 1997;87(12):1944-50.
- 高橋美保子, 丹後俊郎. インフルエンザによる超過死亡の新しい定義とその推定方法の提案. 日本公衆衛生雑誌. 2001;48:402-8.
- 国立感染症研究所感染症情報センター. インフルエンザ流行に伴う超過死亡について. 病原微生物検出情報. 2000;21:265-7.
- 高橋美保子. インフルエンザ流行による超過死亡の範囲の推定 年間死亡率と季節指数を用いた最小超過死亡の推定モデルの応用. 日本公衆衛生雑誌. 2006;53(8):554-62.
- 国立感染症研究所. 報告週対応表 [https://www.niid.go.jp/niid/ja/calendar.html].
- Farrington CP, Andrews NJ, Beale AD, Catchpole MA. A Statistical Algorithm for the Early Detection of Outbreaks of Infectious Disease. Journal of the Royal Statistical Society Series A (Statistics in Society). 1996;159(3):547-63.
- Noufaily A, Enki DG, Farrington P, Garthwaite P, Andrews N, Charlett A. An improved algorithm for outbreak detection in multiple surveillance systems. Statistics in Medicine. 2013;32(7):1206-22.
- EuroMOMO network. [https://www.euromomo.eu/how-it-works/methods/].
- Vestergaard LS, Nielsen J, Richter L, Schmid D, Bustos N, Braeye T, et al. Excess all-cause mortality during the COVID-19 pandemic in Europe - preliminary pooled estimates from the EuroMOMO network, March to April 2020. Euro Surveill. 2020;25(26).
- Nielsen J, Krause TG, Molbak K. Influenza-associated mortality determined from all-cause mortality, Denmark 2010/11-2016/17: The FluMOMO model. Influenza Other Respir Viruses. 2018;12(5):591-604.
- Nielsen J, Mazick A, Andrews N, Detsis M, Fenech TM, Flores VM, et al. Pooling European all-cause mortality: methodology and findings for the seasons 2008/2009 to 2010/2011. Epidemiol Infect. 2013;141(9):1996-2010.
8 補足資料
補足資料3：2012年第1週からの都道府県別の週別の死亡者数（速報値については補正あり・なし両方）。
補足資料4a-d：a-dそれぞれ図1–4の実数値。2017年からの都道府県別と全国の週別の予測死亡者数、および95%片側予測区間（上限）値。
補足資料5：2020年1月から4月までのFarringtonアルゴリズムおよびEuroMOMOアルゴリズムに基づく推定超過死亡上限値（観測死亡数と予測死亡数の差）（補正あり・なし両方）。
9 超過死亡の推定に関するQ&A
10 研究班構成員
「新型コロナウイルス感染症等の感染症サーベイランス体制の抜本的拡充に向けた人材育成と感染症疫学的手法の開発研究」（厚生労働科学研究令和2年度）
| 国立感染症研究所 感染症疫学センター | 鈴木 基 |
| 国立感染症研究所 感染症疫学センター | 砂川 富正 |
| 国立感染症研究所 感染症疫学センター | 高橋 琢理 |
| 国立感染症研究所 感染症疫学センター | 土橋 酉紀 |
| 国立感染症研究所 感染症疫学センター | 小林 祐介 |
| 国立感染症研究所 感染症疫学センター | 有馬 雄三 |
| 国立感染症研究所 感染症疫学センター | 加納 和彦 |
| 東京大学大学院 医学系研究科国際保健政策学 | 橋爪 真弘 |
| 慶應義塾大学 医学部医療政策・管理学教室 | 野村 周平 |
| 聖路加国際大学大学院 公衆衛生学研究科 | 米岡 大輔 |
| 長崎大学 熱帯医学・グローバルヘルス研究科 | Chris Fook Sheng Ng |
| 慶應義塾大学 医学部医療政策・管理学教室 | 宮田 裕章 |
| 早稲田大学 ビジネスファイナンス研究センター | 田上 悠太 |
| 東京工業大学 情報理工学院 | 川島 孝行 |
| 千葉大学 予防医学センター | 江口 哲史 |
| 国立環境研究所 生物・生態系環境研究センター | 瓜生 真也 |
| 東京大学大学院 医学系研究科機能薬理学講座 | 史 蕭逸 |
| 理化学研究所 環境資源科学研究センター | 河村 優美 |
| 株式会社ホクソエム | 牧山 幸史 |
| 株式会社ホクソエム | 松浦 健太郎 |
謝辞： 以下の先生方には、報告書の作成段階でコメントの御協力をいただきました。
（敬称略）
藤田医科大学 衛生学 橋本 修二
東邦大学 医学部 社会医学講座 医療統計学分野 村上 義孝
筑波大学 名誉教授 本田 靖